Ramanujan

Un Génie des Mathématiques

Srinivasa Ramanujan naît en 1887 en Inde. Très jeune, il montre un talent exceptionnel pour les mathématiques. À 16 ans, il développe déjà des théories avancées grâce à un livre de mathématiques : A Synopsis of Elementary Results in Pure and Applied Mathematics.

Malgré son génie, il a des difficultés à l’école. Obsédé par les maths, il néglige les autres matières et perd sa bourse pour le Government College de Kumbakonam. Plus tard, il échoue à entrer à l’Université de Madras pour les mêmes raisons.

Ses débuts en mathématiques

Une santé fragile

Le climat anglais et les restrictions alimentaires dues à la guerre affectent gravement sa santé. En 1919, malade de la tuberculose, il rentre en Inde et meurt en 1920, à seulement 32 ans. Snif.

Un héritage inoubliable

En savoir plus...

Dans le troisième épisode de la série collaborative "Merveilleux Mathématiciens et Mathématiciennes !" des Mathématiciens s'affrontent pour déterminer qui est le meilleur matheux ou la meilleure matheuse de tous les temps. Dans cet épisode, Mathador parle de Ramanujan qui est pour lui le plus génial de tous les mathématiciens.

Exercices

Peu après son arrivée en Angleterre en 1914 Ramanujan a publiée sa formule révolutionnaire pour calculer pi :

\[ \frac{1}{\pi}=\frac{2\sqrt{2}}{9801}\sum_{n=0}^{\infty}\frac{(4n)!(1103+26390n% )}{(n!)^{4}396^{4n}} \]

avec n = 0, on trouve :

\[ \pi\approx\frac{9801}{2\cdot 1103\cdot\sqrt{2}}=3.14159273001\ldots \]

L'erreur est de : $$0.0000000764235\ldots$$

Cette formule est l'une des nombreuses séries infinies qu'il a développées et qui convergent extrêmement rapidement, ce qui les rend particulièrement utiles pour les calculs numériques.

Cette formule a été utilisée bien plus tard, dans les années 60 pour établir des records de précision dans le calcul de pi. Et en 1985, William Gosper utilisa cette formule pour calculer les premiers 17 millions de chiffre de pi.

Avant de calculer Pi avec la formule de Ramanujan, nous allons calculer Pi avec la méthode de Leibniz qui bien que moins rapide, est plus facile à comprendre et à coder.

Objectifs pédagogiques de l'exercice : Prendre en main les boucles et fonctions en Python.

Premier exercice : calculer Pi avec la méthode de Leibniz

L'objectif de cet exercice est d'écrire un programme en Python pour calculer une approximation de Pi en utilisant la méthode de Leibniz.

La méthode de Leibniz repose sur la série suivante :

\[ \pi = 4 \cdot \sum_{k=0}^\infty \frac{(-1)^k}{2k + 1} \]

Ce qui donne ceci :

\[ \pi = \frac{4}{1} - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - \frac{4}{11} + \frac{4}{13} \ldots \]

Chaque terme de cette série ajoute ou soustrait une fraction, et la somme converge lentement vers Pi.

Travail à réaliser :

1. Compréhension de la formule :
2. Implémentation en Python :
   • Écrivez un programme qui calcule une approximation de Pi en utilisant cette formule.
   • Votre programme doit :
     • Demander à l'utilisateur le nombre de termes n à utiliser.
     • Calculer la somme des n premiers termes de la série.
     • Afficher l'approximation obtenue et la comparer avec la valeur réelle de Pi fournie par Python via math.pi.
3. Étapes suggérées :
   • Implémentez une fonction qui calcule un terme de la série.
   • Utilisez une boucle pour calculer la somme des n premiers termes.
   • Affichez le résultat final.

Exemple d’exécution :

Combien de termes voulez-vous utiliser pour calculer pi ? 10
Approximation de pi avec 10 termes : 3.0418396189294032
Valeur réelle de pi : 3.141592653589793

Aller plus loin...

1. Amélioration de la précision :
   • Ajoutez la gestion des décimales avec la bibliothèque decimal.
2. Comparaison :
   • Affichez l’erreur absolue pour montrer la lenteur de la convergence.

Deuxième exercice : Calculer Pi avec la méthode de Ramanujan

L'objectif de cet exercice est de créer un programme en Python qui utilise la méthode de Ramanujan pour calculer une approximation précise de Pi.

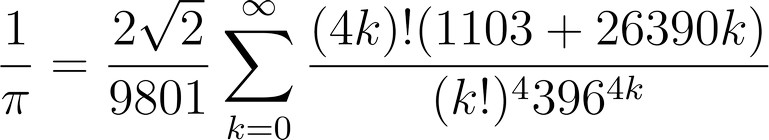
Travail à réaliser :

1. Compréhension de la formule :

2. Implémentation en Python :

   • Écrivez un programme qui calcule une approximation de pi en utilisant cette formule.
   • Votre programme doit :
     • Demander à l'utilisateur le nombre de termes n à utiliser dans la série.
     • Calculer la somme des n premiers termes de la série.
     • Afficher la valeur approchée de (\pi).

3. Étapes suggérées :

   • Écrivez une fonction pour calculer la factorielle.
   • Implémentez une fonction qui calcule le k-ième terme de la série.
   • Implémentez une boucle pour sommer les n premiers termes.
   • Affichez le résultat final.

4. Testez votre programme :

   • Essayez avec différentes valeurs de n (par exemple n=1, 2, 5, 10...)
   • Comparez vos résultats avec la valeur réelle de pi disponible dans Python via math.pi.

---

Exemple d’exécution :

Combien de termes voulez-vous utiliser pour calculer pi ? 3
Approximation de pi avec 3 termes : 3.1415927300133055
Valeur réelle de pi : 3.141592653589793